Bu örneğimiz, konuya çalışırken başlangıç seviyesinde anlaşılması kolay ve aynı zamanda öğrenilmesi gereken önemli konuları da barındırdığı için seçilmiştir. Çalışacağımız Veri setini
buradan indirebilirsiniz.
Uygulama örneklerimiz ile çalışırken genelde Anaconda'da bulunan entegre geliştirme ortamı Spyder'i kullanacağız.
Başlarken Spyder da çalıştığınız dosya ile datasetinizin aynı dizinde olmasını dikkat ediniz. Bunu Spyder default windows layoutunun File_Explorer bölümünden de aynı yerde olup olmadığınızı kontrol edebilirsiniz.
Datasetimizi inceleyecek olursak; Abd 'de 50 adet startup firmanın, yapmış oldukları yatırım harcamaları (Ar&Ge , yönetici giderleri ,pazarlama yatırımları ve bulundukları şehirler) göz önünde bulundurularak, kazançları ölçülmüş. Bu veri seti ile yapacağımız çalışma ile, şirketlerin kazançları ile bu yatırım alanları arasında nasıl bir korelasyon var, hangi yatırım harcaması daha etkili olmuş bunları anlamaya çalışacağız. Veya datasetine bakarak sektöre yeni başlayacak bir firmanın hangi alanlara daha az veya daha fazla bütçe ayırıp yatırım yapması gerekir, bulduğumuz değerlere göre bütçe planlamasında yardımcı olabilecek ipuçlarını görmeye çalışacağız.
Şimdi kullanacağımız kütüphaneleri import ederek başlayalım.
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
verisetimizi de pandas’ın read.csv fonksiyonu ile import edelim.
dataset=pd.read_csv('Startup_Kar.csv')
Datanın tüm satırlarını getirmek istemiyorsanız dataset.head( ) fonksiyonu ile default olarak ilk beş satırı veya kaç satır getirmek istiyorsanız parantezin içerisinde belirterek sağ alt köşede IPython console de görebilirsiniz.
Burada bağlı ve bağımsız değişkenleri tanımlıyoruz:
Çoklu Lineer denklemi
\[
y=a_0 +a_{1}X^1+ a_{2}X^2 +a_{3}X^3+a_{4}X^4
\]Buradaki X değerleri (R&D, Administration, Marketing Spend, State) bağımsız değişkenlerdir. Aynı zamanda predictor olarakta adlandırılırlar, y ise bağlı değişkenimizdir. (profit) denkleme eklenecek her X değeri için alacağı değer farklılık gösterir.
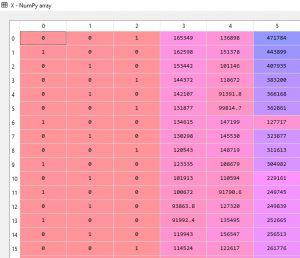
X ve y değişkenlerimizi aşağıdaki gibi tanımlıyoruz. iloc fonksiyonu ile [:,:-1] şeklinde belirttiğimizde tüm satırları ve sütun olarak en son sütün hariç tüm değerleri alsın istiyoruz. y için ise index numarası 4 olan profit kolon dur. Sadece bu kolonu almasını sağlıyoruz.
X=dataset.iloc[:,:-1].values
y=dataset.iloc[:,4].values
Makine öğrenmesi algoritmaları hesaplama yaparken sayısal değerler üzerinden hesap yaptığından kategorik değerleri bu forma dönüştürmemiz gerekir. X matrisinde bulunan state kolonu kategorik özelliktedir. Diğer kolonlardakiler ise sayısal olarak verilmiştir. Kategorik değerimizi algoritmamızın anlayacağı sayısal forma dönüştürmek için sklearn.preprocessing kutuphanesinin LabelEncoder Class ını kullanıyoruz.
from sklearn.preprocessing import LabelEncoder,OneHotEncoder
labelencoder=LabelEncoder()
X[:,3]=labelencoder.fit_transform(X[:,3])
onehotencoder=OneHotEncoder(categorical_features=[3])X=onehotencoder.fit_transform(X).toarray()
state kolonu index olarak 3. index te bulunuyor. labelencoder nesnesine fit_transform metodu ile bu kolonu dönüştür , fit et diyoruz.
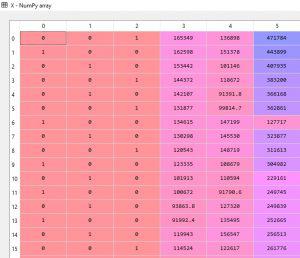
Burada Dummy variable (Kukla değişkenlerimiz oluştu). Artık şehir adları sayısal değerlere dönüştürülmüş ve bir satırdaki değerler hangi şehre ait ise o kolon bir, diğerleri sıfır değeri ile gösterilecektir. Ör: 1. satırdaki değerler 2 nolu indexte yer alan New York şehrine ait olduğundan o kolon 1 ,diğerleri 0 dır. Modelin, bu değerler arasında yani 2 büyüktür 1 veya 0 +1 2 den küçüktür gibi bir ilişkisel değerlendirme veya sıralama yapmasını istemiyoruz. bu durumu engellemek için OneHotEncoder classını kullanıyoruz. Yalnız yapılan her işlem başka tür probleminde oluşmasına sebep olmaktadır.
Dummy variable Trap( Kukla değişken tuzağı)
Linear regression modellerinde en sık karşılaşılan problem türüdür. Multicollinearity dediğimiz çoklu bağlılık problemine neden olur. Multicollinearity bir değişkeni tahmin eden en az iki değişken arasında çok yüksek ilişkinin olması durumudur. Kukla değişkenler aynı zamanda indikatör olarak da adlandırılırlar. Modelde bazı parametleri doğru tahmin etmeyi engeller ve modele ek bir bilgi vermez. Bunun için oluşan kukla değişkenlerden herhangi birini modele dahil etmeyip çıkartmamız gerekir.
Aşağıdaki gibi yeni X matrisini kukla değişkenlerden en baştakini (index numarası sıfır olan kolon ) almadan yeniden oluşturuyoruz. Normalde bunu model otomatik anlıyor ve düzeltiyor. Biz burada konuyu açıklamak için belirttik.
X=X[:,1:]
Datalar artık model için eğitim ve test amaçlı ayrıştırılmaya hazır duruma gelmiştir. Bunun için de sklearn.cross_validation kütüphanesinin train_test_split classını kullanıyoruz.
from sklearn.cross_validation import train_test_split
X_train,X_test,y_train,y_test= train_test_split(X,y,test_size=0.2,random_state=0)
spyder'da bir classın hangi paremetreler aldıgına CRTL+I tuşlarına basıp görebilirsiniz.
train_test_split classı da train ve test dataları oluşturmak için X ve y parametrelerinin girilmesi ve test_size ı tanımlanmasını istiyor. Genelde test_size %20, %30 olarak tanımlanır. Çoğunluk train datalarına ayrılsınki modelimizin eğitim dataları ile değişkenler arasındaki korelasyonu doğru hesaplasın ve tahminlerini en az hata ile yapsın. (Ör: veride 100 adet sample varsa 20 si test , 80 i eğitim için ayrılabilir.) Random_state parametresi de sıfır olarak verilmesinin sebebi farklı zamanlarda bu veri setleri ile çalışırken aynı eğitim ve test datalarını alıp modele uygulasın.
Model oluşturma
Artık eğitim ve test dataları hazır. Şimdi modelde kullanacağımız oluşturup LinearRegression classını bir objeye tanımlıyoruz. Eğitim datalarını modele verip fit ettik. Burada LinearRegression u bir makine olarak kabul edelim, train datalarını bu makineye tanımlayarak makinenin X ve y arasında ilişkiyi öğrenmesini sağladık. Test datalarını modelin güvenilirliğini görmek için test amaçlı kullanacağız.
from sklearn.linear_model import LinearRegression
regressor=LinearRegression()
regressor.fit(X_train,y_train)
X_test dataları ile oluşturdugumuz modelin düzgün tahmin edip etmediğini modelimizin gercek değerlere yakın tahminler yapıp yapmadığına bakmak icin predict metodunu kullanıyoruz
y_pred=regressor.predict(X_test)

Datanın tüm satırlarını getirmek istemiyorsanız dataset.head( ) fonksiyonu ile default olarak ilk beş satırı veya kaç satır getirmek istiyorsanız parantezin içerisinde belirterek sağ alt köşede IPython console de görebilirsiniz.
Burada bağlı ve bağımsız değişkenleri tanımlıyoruz:
Çoklu Lineer denklemi
\[
y=a_0 +a_{1}X^1+ a_{2}X^2 +a_{3}X^3+a_{4}X^4
\]Buradaki X değerleri (R&D, Administration, Marketing Spend, State) bağımsız değişkenlerdir. Aynı zamanda predictor olarakta adlandırılırlar, y ise bağlı değişkenimizdir. (profit) denkleme eklenecek her X değeri için alacağı değer farklılık gösterir.
X ve y değişkenlerimizi aşağıdaki gibi tanımlıyoruz. iloc fonksiyonu ile [:,:-1] şeklinde belirttiğimizde tüm satırları ve sütun olarak en son sütün hariç tüm değerleri alsın istiyoruz. y için ise index numarası 4 olan profit kolon dur. Sadece bu kolonu almasını sağlıyoruz.
X=dataset.iloc[:,:-1].values
y=dataset.iloc[:,4].values
Makine öğrenmesi algoritmaları hesaplama yaparken sayısal değerler üzerinden hesap yaptığından kategorik değerleri bu forma dönüştürmemiz gerekir. X matrisinde bulunan state kolonu kategorik özelliktedir. Diğer kolonlardakiler ise sayısal olarak verilmiştir. Kategorik değerimizi algoritmamızın anlayacağı sayısal forma dönüştürmek için sklearn.preprocessing kutuphanesinin LabelEncoder Class ını kullanıyoruz.
from sklearn.preprocessing import LabelEncoder,OneHotEncoder labelencoder=LabelEncoder()X[:,3]=labelencoder.fit_transform(X[:,3])
onehotencoder=OneHotEncoder(categorical_features=[3])
X=onehotencoder.fit_transform(X).toarray()
Onehotencoder Da fit_transform X ‘i bir parametre gibi algılıyor. Onu tekrar dizin haline getirmek için sonuna toarray() ekleyip yeni X e eşitledik.

Burada Dummy variable (Kukla değişkenlerimiz oluştu). Artık şehir adları sayısal değerlere dönüştürülmüş ve bir satırdaki değerler hangi şehre ait ise o kolon 1 diğerleri 0 değeri ile gösterilecektir. Ör: 1. satırdaki değerler 2 nolu indexte yer alan New yok şehrine ait oldugundan o kolon 1 ,diğerleri 0 ile gösterimiştir. Yalnız modelin, bu değerler arasında yani 2 büyüktür 1 veya 0 +1 2 den küçüktür gibi bir ilişkisel değerlendirme veya sıralama yapmasını istemiyoruz. bu durumu engellemek için OneHotEncoder classını kullanıyoruz. Yalnız yapılan her işlem başka tür probleminde oluşmasına sebep olamktadır.
Dummy variable Trap( Kukla değişken tuzağı)
Linear regression modellerinde en sık karşılaşılan problem türü. Multicollinearity dediğimiz çoklu bağlılık problemine neden olur. Modelde bazı parametleri doğru tahmin etmeyi engeler ve modele ek bir bilgi vermez. Bunun için oluşan kukla değişkenlerden herhangi birini modele dahil etmeyip çıkartıyoruz.
Aşağıdaki gibi yeni X matrisini kukla değişkenlerden en baştakini (index numarası sıfır olan kolon ) almadan yeniden oluşturuyoruz.
X=X[:,1:]
Datalar artık model için eğitim ve test amaçlı ayrıştırılmaya hazır duruma gelmiştir. Bunun için de sklearn.cross_validation kütüphanesinin train_test_split classını kullanıyoruz.
from sklearn.cross_validation import train_test_split
X_train,X_test,y_train,y_test= train_test_split(X,y,test_size=0.2,random_state=0)
spyder'da bir classın hangi paremetreler aldıgına CRTL+I tuşlarına basıp görebilirsiniz.
train_test_split classı da train ve test dataları oluşturmak için X ve y parametrelerinin girilmesi ve test_size ı tanımlanmasını istiyor. Genelde test_size %20, %30 olarak tanımlanır. Çoğunluk train datalarına ayrılsınki modelimizin eğitim dataları ile değişkenler arasındaki korelasyonu doğru hesaplasın ve tahminlerini en az hata ile yapsın. (Ör: veride 100 adet sample varsa 20 si test , 80 i eğitim için ayrılabilir.) Random_state parametresi de sıfır olarak verilmesinin sebebi farklı zamanlarda bu veri setleri ile çalışırken aynı eğitim ve test datalarını alıp modele uygulasın.
Artık eğitim ve test dataları hazır. şimdi modelimizi oluşturup classı regressor olarak bir objeye tanımlayıp eğitim datalarını verip modele bu dtaları fit ettik. Burada LinearRegression u bir makine olarak kabul edeim, train dtalarını bu makineye tanımlayarak makinenin X ve y arasında ilişkiyi öğrenmesini sağladık. Test datalarını da bu modeli ne derecede öğrendiğini test edip görmek için kullanacağız.
from sklearn.linear_model import LinearRegression
regressor=LinearRegression()
regressor.fit(X_train,y_train)
X_test dataları ile oluşturdugumuz modelin düzgün tahmin edip etmediğini modelimizin gercek degerlere yakın tahminler yapıp yapmadığına bakmak icin predict metodunu kullanıyoruz
y_pred=regressor.predict(X_test)
uraya kadar tüm x değerlerini alarak y yi tahmin etmeye çalıştık. Acaba bu model istenilen düzeyde optimum bir model mi? Her değişkeni denkleme koymak gerekli mi veya faydalı olur mu ? Burada bu farkı anlamak için başka bir model daha kullanacağız. Yalnız bir lineer model oluşturmadan önce aşağıdaki 5 özelliğin doğruluğundan emin olunmalı. Bu konulara ileriki günlerde ayrıntılı olarak değinilecektir.
Lineer Regresyon Varsayımları
- 1.Linearity
- 2.Homoscedasticity
- 3.Multivariate normality
- 4.independence of eros
- 5.Lack of multicollinearty
Model oluşturma
Yukarda yapmış olduğumuz çalışmada y(profit)’i tahmin etmek için bir çok X değişkeni vardı. Modele başlamadan önce bunlardan hangilerini seçmemiz hangilerini yok etmemiz gerektiğini belirlememiz gerekir.
Tüm değişkenleri modele alırsak doğru çalışmayabilir. Ya da bir gün şirketinizin ceo suna sunum yapmak istediğinizde bu değişkenlerden tek tek bahsetmek sunumun pratik olmasını sağlamayacaktır. Amacımız burada hangi değişkenlerin çok çok önemli olduğunu belirleyip modelimize bu değerleri almak.
Model inşa etmenin 5 yöntemi (1.All-in ,2.Backward Elimination, 3.Forward Selection, 4.Bidirectional Elimination,5.Score Comparison ) var. Bunlardan ileride ayrıntılı bahsedeceğim, burada sadece örneğe uygun olduğu için backward elimination modelini kullanacağız.
Backward Elimination:
- 1. adım: Bir önem seviyesi seç . Genelde SL=0.05 seçilir.
- 2. adım: Modelde kullanılacak tüm X leri modele fit et.
- 3. adım: En yüksek P-value değerine sahip X i seç .Eğer bu değer 0.05 ‘ten büyükse 4.adıma geç , değilse modeli çalıştırmayı durdur. Model hazır demektir.
- 4. adım. Bulduğun En yüksek p-value değerini modelden çıkart
- 5. adım: geriye kalan X leri modele fit edip tekrar çalıştır.
Burada statsmodel.formula.api kütüphanesini kullanacağız.
import statsmodels.formula.api as sm
Statsmodel
\[
y=a_0 +a_{1}X^1+ a_{2}X^2 +a_{3}X^3+a_{4}X^4
\]denklemindeki a
0 sabitlerini içermediğinden modele manuel olarak bunların tanımlanması gerekir. Bu da şu şekilde olur. Normalde a
0 a
0X
0 şeklindedir. X
0’lar ın değeri 1 olduğundan yazılmaz. Denklemde a
0 ları tutmak için bu X’leri tanımlamamız gerekir. Bunu da numpy.append fonksiyonunu kullanarak yapacağız.
Append fonksiyonunun aldığı parametreleri CTRL+I ile görebilirsiniz. Normalde sıralama
X=np.append(arr=np.ones((50,1)), values=X, axis=1) şeklindedir. Bu sıralamaya göre yaparsak 1 ler en sona eklenecek. Biz en başa eklemesini istediğimizden X ile np.ones ın yerlerini değiştirdik.
X=np.append(arr=X, values=np.ones((50,1).astype(int), axis=1)
Bundan sonra artık yeni bir matris oluşacak bu matrisi de X_opt diye tanımlayalım.
X_opt=X[:,[0,1,2,3,4,5]]
Burada yeni bir regressor oluşturmamız gerekiyor. Çünkü bir önceki modelimizin regressoru linearRegressor classına aitti. Bu regressor statsmodel’e ait olacak. Bunun için burada kullanacağımzı classın adı OLS (Ordinary Least Square). Aldığı parametreleri yine kontrol ederek ayrıntıları okuyabilirsiniz.
Regressor_OLS=sm.OLS(endog=y,exog=X_opt).fit()
regressor_OLS.summary()
regressor_OLS.summary() ile de tablonun özetini getirmesini istiyoruz.
Artık backward elimination modelini adım adım uygulayabiliz
X_opt=X[:,[0,1,2,3,4,5]]
regressor_OLS=sm.OLS(endog=y,exog=X_opt).fit()
regressor_OLS.summary()
X_opt=X[:,[0,1,3,4,5]]
regressor_OLS=sm.OLS(endog=y,exog=X_opt).fit()
regressor_OLS.summary()
X_opt=X[:,[0,3,4,5]]
regressor_OLS=sm.OLS(endog=y,exog=X_opt).fit()
regressor_OLS.summary()
X_opt=X[:,[0,3,5]]
regressor_OLS=sm.OLS(endog=y,exog=X_opt).fit()
regressor_OLS.summary()
X_opt=X[:,[0,3]]
regressor_OLS=sm.OLS(endog=y,exog=X_opt).fit()
regressor_OLS.summary()
Görüldüğü gibi En son Ar-ge kaldı . Burada belki marketing harcamalarını da denkleme alınır. Alınıp alınmayacağı R-squared , Adj. R-squared gibi değerlerede bakılarak belirlenebilinir. Veya daha gelişmiş istatistik yöntemlerle F-static gibi yöntemler kullanılarak karar verilir.
dataset.corr() ile ayrıca değişkenler arasında hangilerinde yüksek korelasyon var görebilirsiniz.
Sonuç olarak
Görüldüğü gibi en yüksek korelasyon Ar-Ge de. Daha sonra marketing harcamaları kısmında.
Diğer değişkenlerin aslında kazanca çok büyük etkisi yokmuş. Pazara girecek yeni bir start-upın Ar-Ge sini ve marketing çalışmalarını iyi yaparsa yüksek kazanç elde edebileceğini söyleyebiliriz.