Bunlardan bir kesimi belli bir düzenek öğrenmesi(makine öğrenmesi) için kullanılırken bir kesimi birden çok yerde kullanılabilir. Bunların sayısı yüzlerce, küçük değişiklikler yapılmış sürümleri de sayılırsa binlerce olabilir. Burada çok bilinenlerinin ne olduğu kısaca açıklanacaktır. Buradaki açıklamalardan algoritmaları tümüyle anlamak olanaklı değildir, yalnızca ne oldukları konusunda genel bir bilgi verilmektedir.
Yapay Sinir Ağı (Artificial Neural Network)
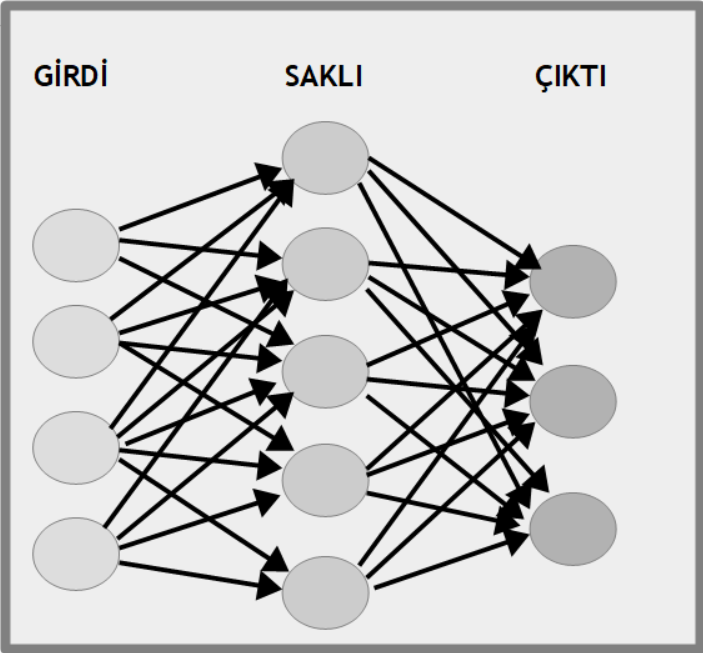
Gözetimli öğrenme yöntemlerinden birisinin adı da yapay sinir ağı (artificial neural network) adını taşır. Bu adı verilmesinin nedeni canlılardaki sinir ağlarına benzetilmesidir ki bu benzerlik de çoğu kişi için tartışmalıdır. Bu algoritmayla hem sınıflandırma (classification) hem de salkımlama (clusering) yapılabilir. Bu yöntemde veri kümesi bir girdi (input) olarak kabul edilir ve her veri noktasının hangi sınıfa girdiği de bir çıktı (output) olarak algılanır. Girdideki her noktanın çıktıdaki noktaya olan etkisine ağırlık (weight) adı verilir. Örneğin insanların el yazısıyla girdiği sayıları anlamaya yarayan bir öğrenme düzeni tasarlayalım. Öncelikle daha önce el yazısıyla yazılımış 10 adet sayamak (digit) imgesi düzene girilir. Sonra bu imgelerdeki her benek (pixel) rakamın hangisi olduğunda bir ölçüde etkilidir. Öncelikle her beneğin her sayamak için etkisi bir ağırlık olarak alınır ve rasgele verilir. Sonra ne ölçüde doğru olduğuna bakılır. Şu andaki verilen ağırlık gerçek etkiden fazla sonuç çıkmasını sağlıyorsa azaltılır, eksik sonuç çıkmasını sağlıyorsa artırılır. Başka bir deyişle önce girdiğin çıktıya etkisi uydurulur ve sonuçların yanlışlığına bakılarak doğru yönde değiştirilir. Bu işlem girdinin çıktıya etkisini doğruya yakın olana dek sürdürülür. Ara aşamalar henüz doğru sonucu vermediği için saklı (hidden) tutulur. Arada kaç saklı aşama olacağı doğruluğa ulaşmak için ölçütün ne olduğuna doğrudan bağlıdır. Rakam türü girdilerde 4 ve 7 değerlerini örnek olarak alalım. 4 sayamağı için sol alt, sol üst köşelerdeki beneklerin boş, sağ üst ve sağ alt köşelerdeki beneklerin dolu olması gerekir. 7 sayamağı için de sağ alt ve sol alt köşedeki benekler boş, sağ üst ve sol üst köşedeki benekler doludur. Dolayısıyla, sol üst köşedeki benekler için 4 ve 7 rakamının değerleri başlangıçta ne olursa olsun, sonuçta sol üst köşedeki beneklerin 4 için sıfıra yaklaşırken 7 için 1'e yaklaşır. Başka bir deyişle, yapay sinir ağları, verilerin hangi kesiminin sonuçtaki sınıflandırmada ne ölçüde etkili olduğunu deneyerek ve yanlışlarından öğrenerek bulur. Her denemeden sonra yanlış olan değeri daha doğru değerle değiştirirerek doğruya ulaşır.
K-En Yakın Komşu (K-Nearest Neighbour)
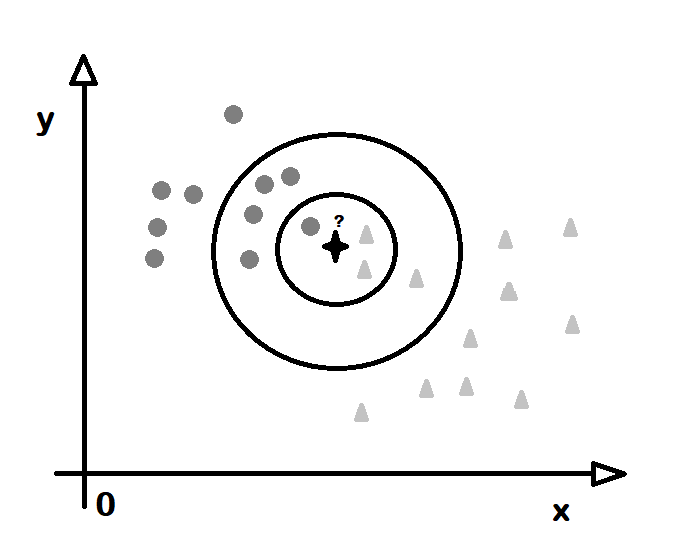
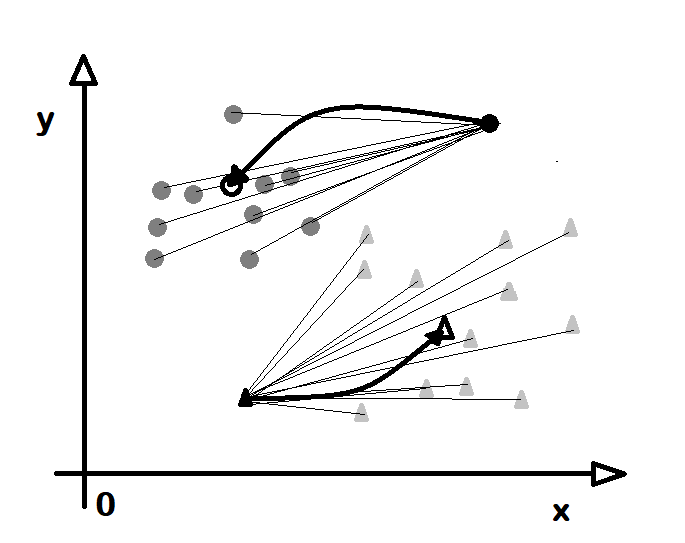
Düzenek öğrenmesinde gözetimli öğrenme türüne giren sınıflandırma (classification) algoritmalarından birisi de k-en yakın komşu (k-nearest neighbour) adını alır. Temel mantığı, bir noktanın hangi sınıfta olduğunu, kendisine yakın belli sayıda noktaların hangi sınıfa ait olduklarına bakılarak bulunmasıdır. Buna göre bir noktanın 10 komşusundan 2 adedi A sınıfına, 7 adedi B sınıfına 1 adedi de C sınıfına aitse bu durumunda o noktanın B sınıfına ait olduğu sonucuna varılır. Burada komşu (neighbour) bir noktaya en yakın, uzaklığı en az olan noktalar anlamına gekir. Burada uzaklık (distance) hesaplama yöntemi dışarıdan bildirilir. Örneğin iki boyutlı veride iki nokta P1 (x1,y1) ve P2 (x2,y2) olsun. Aralarındaki uzaklık x değerleri arasındaki uzaklğını saltık (absolute) değerleri ile y değerleri arasındaki uzaklığın saltık değerlerinin toplamı olabilir. Ya da üçgenden yola çıkılarak uzaklık koordinatlar arasındaki farkların karalerinin toplamının karekökü olabilir. Bir noktanın bir noktaya olan uzaklık değerinin hesaplama yöntemi belirlendikten sonra bakılacak komşuların sayısı bilinmelidir. Buradaki k sayısı, k sayıda komuşunun hangi sınıfa girdiğine bakılacağını bildirir. O yüzden k sayısının seçilmesi kimi durumlarda sonucu değiştirir. Örneğin 5 komşudan 3 tanesi X sınıfına giriyor diye noktanın X olduğu düşünülebilir ancak k değeri 10 alınırsa ve 3 tane X, 5 tane Y bulunursa bu durumda noktanın Y olduğu düşünülür. Komşu sayısı 20 olursa ve 3 tane X, 5 tane Y varkan 9 tane Z komşusu varsa bu durumda da nokta Z kümesine girer. O yüzden sonucu pek fazla değiştirmeyen bir K değeri seçilir.
İlkesel Bileşen Çözümleme (Principal Component Analysis)
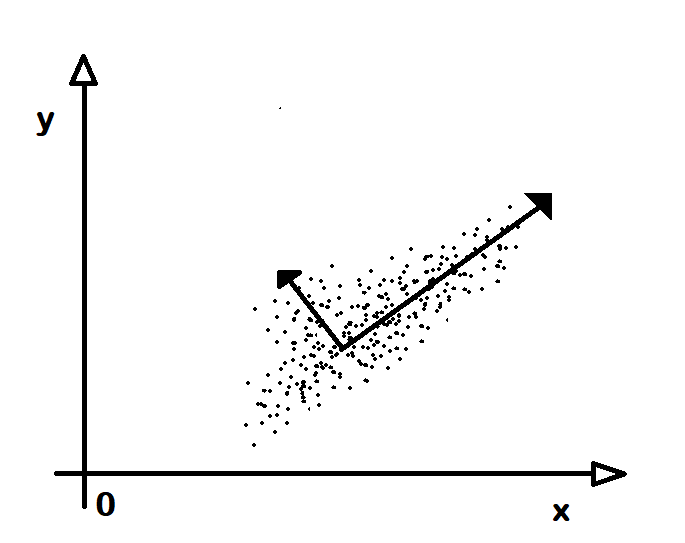
Birden çok boyuttan oluşan verilerden veriler arasında belli bir ilinti (corelation) olabilir. Örneğin insanların boyları ve kiloları birer boyut olsun. İnsanların boyları arttıkça kiloları da artacağı açıktır. Bu durumda bir insanın cinsiyetine ya da yaşına karar verirken doğrudan kilo ve boy değerlerini kullanmak doğru olmayabilir. Çünkü ikisi arasında çoktan bir ilişki var. Genç yaştaki bir erkek ile olgun yaştaki bir kadının kilosu aynı olabilir. Bu gibi durumlarda kökendeki boyut değerlerine bir dönüşüm uygulanarak yeni boyutlar elde edilir. Artık bu yeni boyutlar birbiriyle ilintili değildir ve karar vermekte kullanılmaya daha uygun olur. Ancak bu dönüşümün yapılabilmesi için yeni boyutların eksen (axis) konumları bulunmalıdır. İşte, dönüşümün taban alınacağı eksenleri bulma işlemine ilkesel bileşen çözümleme (primary component analysis) denir. Her bir eksene de bileşen (component) adı verilir. Bu yöntemde yeni eksenlerden hangisinin daha önemli olduğu, daha doğru bir deyişle, hangisinde verilerin değişkenlik sunduğu bulunur. En çok değişkenlik bulunan bileşen en önemlisi, ötekilerde buna göre sıralarak elde edilir. Buna göre öncelikle en çok değişlenlik gösteren dönüştürülmüş boyuta göre öncelikli kararlar verilir.
Destek Yöney Düzenekleri (Suppor Vector Machines)
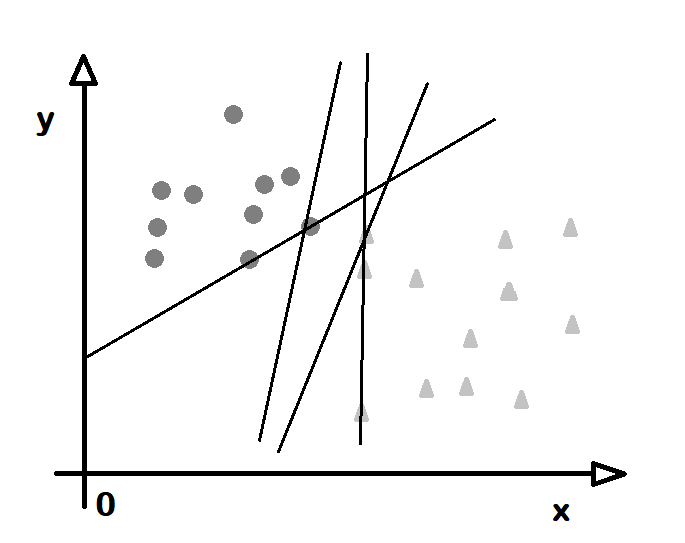
Düzenek öğrenmesinde sınıflandırma (classification) ve gerileme (regression) işlemi için destek yöneyi (support vector) adı verilen yapılar kullanır. Bunlar, bir çok boyuttan oluşan uzayı bölen çizgi ve düzlemlerdir. Kaç boyut varsa bir eksiği boyutta tanımlanırlar. Örneğin iki boyutlu bir veride bir çizgi çizilir ve belli bir sınıf bu çizginin bir yakasında kalırsa bu bir destek yöneyidir. Her sınıf için bir destek yöneyi bulunur ve yeni bir değer verildiğinde bu değerin hangi sınıfta olduğu bu yöneye göre belirlenir. Boyut sayısı 3 olunca destek yöneyi bir düzlem olur. N boyutlu bir düzende, uzayı bölen yöneye aşırıdüzlem (hyperplane) adı verilir. Dolayısıyla destek yöneyleri uzayı bölen aşırıdüzlemlerden oluştur. Kimi durumlarda bir sınıfa ait noktalar bir arada olsalar da başka sınıfların içinde ya da çevresinde olabilir. Bu durumda araya bir düzlem koymak olanaksız gibi görünebilir. Bu durumda evin (kernel) adı verilen işlevler kullanılır. Noktalara öyle bir dönüşüm uygulanır ki artık hepsi bir düzlemin bir yakasında kalır.
Toy Bayes'çi Sınıflayıcı (Naive Bayesian Classifier)
Bir veri kümesinde hangi noktanın hangi sınıfa girdiğini olasılık (probabilty) kuramlarından Bayes kuramına göre bulan algoritmaya toy bayes'çi sınıflayıcı (naive bayesian classifier) adı verilir. Bayes kuramı, daha önceden bir kaç olay arasında ilişki görünmesi durumunda, sonraki olaylarında aynı değerlere bakarak var olan ilişkilerinin bulunmasıdır. Örneğin gönderilen bir e-postanın değersiz (spam) olup olmadığını anlamak için insanların daha önce değersiz olarak işaretlediği e-postalardaki sözcüklere bakılır. Örneğin "ikramiye kazandınız" gibi bir tümce hep değersiz e-postalarda çıkıyor da gerçek kişilerin gönderdiklerinde hiç çıkmıyorsa içerisinde sözkonusu sözcüklere geçen e-postaların değersiz olma olasılığının yüksek olduğu söylenebilir. Buna göre bir yazının içindeki sözcüklerin sıklık (frequency) bilgileri bulunur ve değersiz e-postalarınkiyle karşılaştırılır ve değersiz olma olasılığı bulunur. Bu yönteme toy (naive) denmesinin nedeni, gerçekte ilişkisiz de olsa yakın konumlarda bulunan verileri ilişkili sanabilmesidir. Örneğin beslenen verilerdeki değerlere eşit ele alış göstermekte boyutlardan hangisinin daha önemli olduğuna bakmamasıdır. Burada anlatılan dışında olasılık sınıflayıcı (probabilty classifier) türleri de vardır ve bunlar daha gelişmiş olasılık modellerine göre sınıflandırma yaparlar.
\( P (C|A)=\frac{P(A|C)P(C)}{P( A )} \)K-Bayağılar Salkımlama (K-Means Clustering)
Bu yöntem salkımlamada bayağı (mean) adı verilen, aritmetik ortalama (average) gibi değerlere bakılarak bir noktanon hangi sınıfa girdiğine karar verilir. Buradaki k harfki k adet sınıf olacağının baştan verileceği anlamına gelir. O yüzden bu algoritmaya k-bayağılar salkımlama (k-means clustering) adı verilir. Bu yöntemde bir bayağı değere yakın olanlar o bayağı değerin özeğinde bulunduğu sınıfın bir parçası sayılırlar. Başka bir deyişle, bir nokta kime yakınsa onunla birlikte olur. Bu yöntemde bayağı değerlerin sayısı baştan bellidir ancak kendileri baştan belli değildir. O yüzden öncelikle rasgele bayağı değerler bulunur. Sonra her noktanın bu bayağı değerlere olan uzaklığı alınır ve yakın olan noktalar o sınıfa konur. Sonra noktaların eklendiği sınıfların yeni bayağı (mean) değerleri, örneğin aritmetik ortalaması alınır. Sonra bu yeni bayağılara göre her noktanın uzaklığı hesaplanırve her nokta kendisine en yakın olan bayağının sınıfına sokulur. Bu süreç, tüm noktalar aynı yerde kalana dek, yani yer değişmeler bitene dek sürer. Başlangıçta bir nokta belli bir bayağının sınıfına girer ancak bir süre sonra yeni bayağı ondan uzaklaşabilir ve o da başka bir sınıfa girer. Son durumda hem bayağılar sınıflarındaki noktalara en az uzaklıkta bulunmuş olurlar hem de her nokta kendisine en yakın bayağının sınıfına girmiş olur. Burada anlatılan yöntemin ortanca (median) değerine bakarak karar verildiği k-ortancalar salkımlama (k-medians clustering) adı verilen bir değişiği de bulunmaktadır.
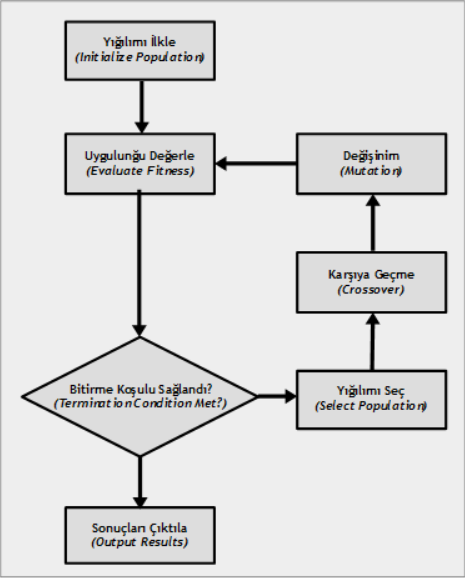
Genetik Algoritmalar (Genetic Algorithms)
Biyolojideki evrim kuram (evolution theory) dirilerin türlülüğünü açıklamaya yaramaktadır. Buna göre dirilerin kimi bireylerinde genlerinde rastgele bir değişinim (mutation) olur. Daha sonra bu değişinime uğrayan bireylerden çevreye uygun olanlar doğal seçilim (natural selection) ile çoğalırken uygun olmayanlar giderek yok olur. Uzun süre geçtikten sonra bu değişinimler sonucunda her yinelenme (iteration) daha iyiye doğru gider. İşte genetik algoritmalar (genetic algorithms) de bu yöntemle sonuçlar üretir. Genellikle eniyileme (opimization) ve arama (search) konularında işlev görürler. Buna göre önce derneşim (permutation) ile rasgele bir öbek sonuç üretilir. Sonra her sonucun ne denli doğruya yaklaştığına bakılır. Sonra doğruya en uzak olanlar atılır ve yeni değerler daha doğru olanlardan oluşan katışım (combination) olarak yeniden üretilir. Buna karşıya geçme (cross over) adı verilir. Yine oluşan durumlardan her birinin doğruluğu sınanır ve yine doğruya uzakların atıldığı yakınlardan katıştırılarak sonuçların üretildiği işlemler yinelenmeli olarak, en doğru sonuç bulunana dek sürdürülür. Bu algoritma olabilecek eniyi (optimum) sonucu her durumda vermez ancak ilişkin olarak daha uygunları bulabilir.
Bu konularda ayrıntılı bilgi, kurs, özel ders, uzaktan eğitim, ödev ve proje destek, kitap ve video için tıklayın :
Python Business Intelligence, Data Science ve Machine Learning




